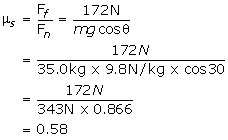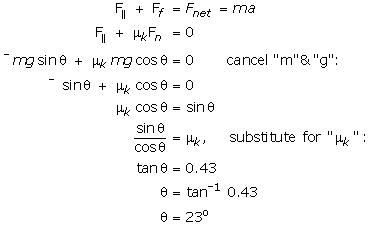Lesson
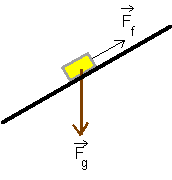
In the previous lesson we applied Newton's Laws to objects moving horizontally and objects moving vertically. (To refresh your memory on the vertical applications, just recall the practice exercises on the elevator and the sanding block on a wall.) In this lesson we will deal with objects on ramps or inclined planes. Practice exercise 1In this exercise we will draw a free body diagram that describes a block sliding down an inclined plane. The object is to identify all the forces and the components of the forces perpendicular to and parallel to the plane. |
|
|
Although our still picture may not suggest it at first, you must realize that the block is actually sliding down the plane. If this were not the case, the friction force would not be acting up the plane! Can you see what makes the block slide down? If not, go to the next picture. |
 |
Since gravity pulls straight downward to the centre of the earth, a component of the weight lies along the plane (see orange vector). We will call this F-parallel or
This force is causing the block to slide. |
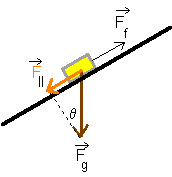 |
Of course, if the angle were smaller, then the orange vector would be smaller and the block might just sit there. Why would it sit there? Because of friction. And friction requires a normal force. Can you see what causes the normal force? Go to the next picture for the answer. |
|
You should be saying to yourself that this picture doesn't really show the normal force. However, we do see a perpendicular force |
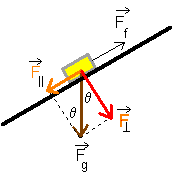 |
|
The normal force is the reaction force (equal and opposite in direction) to Fn = mg cos θ. |
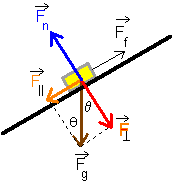 |
|
The final picture in this exercise has the trigonometric terms written in it. |
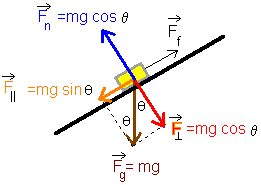 |
Practice exercise 2This exercise has two animations that you can interact with. By clicking on the step button at the bottom of the first picture you will work through (in a slightly different way) the information that was presented in Practice exercise 1.
Up to this point point in time we have not said why it is that the angle between the plane and the ground is the same as the angle between the perpendicular and parallel components of weight vector. The next interactive animation show this is so.
|
|
Practice Exercise 3A bundle of shingles sits on a plank while a worker raises one end so that the shingles slide down the plank to a co-worker at the other end. At the very, very instant that the shingles are about to slide, the plank makes an angle of 30o with the ground. If the mass of the bundle is 35.0 kg, what is the coefficient of static friction? SolutionStep 1--read and understand the story of the problemDo you remember how, in primary and elementary school, you use to put your eraser on your ruler and then raise one end of your ruler until the eraser started to slide? This exercise is like that. Step 2--list the givens and the unknownm= 35.0 kg g = -9.8 N/kg (you will probably be more comfortable if we dispense with the negative for "g". You will see what we mean as you do the exercise.) θ = 30o μs= ? Step 3--plan a strategy |
|
| You have to get a feeling for that tiny, tiny instant of time when the shingles are about to move. It is then that the component of the weight down the plane just balances the force of friction up the plane. That is, |
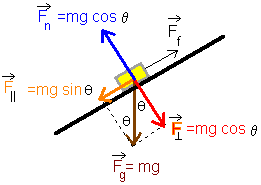 |
|
If down the plane is negative and up the plane is positive, then, strictly speaking we should be writing Step 4--carry out the planFirst find the frictional force:
Back to the problem. Since 172 N is the frictional force just as the bundle starts to move, we can compute the coefficient of static friction:
Step 5--communicateThe coefficient of static friction is 0.58. Let's do another... |
|
Practice exercise 4Continuing with the story in exercise 3, what will be the acceleration if the plank is raised to an angle of 45o with the ground and μk = 0.43? Step 1--Read and understand the problemIf you do a rough sketch you will see that increasing the angle makes the component Step 2--list the givens and the unknownm= 35.0 kg g = 9.8 N/kg θ = 45o μk= 0.43 a = ? Step 3--plan a strategy |
|
| It will help to draw a picture. If you compare it with the 30o pictures above, you will see that the only magnitude which hasn't changed is Fg. We will set up equations for the net force in the parallel direction, and solve for "a". | 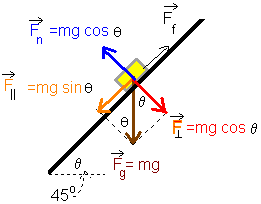 |
Step 4--carry out the planΣ (parallel forces) = Next, substitute for
Step 5--communicateThe angle that allows constant speed down the plane is 23o. Isn't it interesting that for our givens the plank had to be lowered by 7o to maintain constant speed once the motion had begun? Isn't it also neat that for zero acceleration μk = tan θ? You will re-visit this idea when you do the laboratory activity in Lesson 06. Let's do another... |
|
Practice exercise 6
The bundle of shingles could only slide on the incline due to its weight. What about an object that is powered up (or down) and incline? For example, consider the overzealous student who may have taken his physics project too seriously (see picture below).
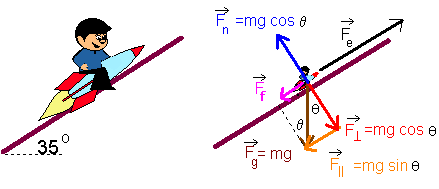
The combined mass of himself and his rocket is 1200 kg. The coefficient of kinetic friction between the rocket and the ramp is 0.60. His intention was to design a rocket to cause an acceleration of 5g's up the ramp. What must be the thrust of the rocket engine?
Step 1--read and understand the story of the problem
This is a scary story so we don't want to dwell on it too long. Look at the free-body diagram. Here's what you should notice: friction is down the plane because the rocket is going up; the force up the plane is the force of the engine (Fe); to reduce clutter the orange parallel component of the weight has been shifted to a new location.
Step 2--list the givens and the unknown
m = 1200 kg
θ = 35o
μk = 0.60
a = 5g = 5 x 9.8 m/s2 = 49 m/s2 or 49 N/kg
Fe = ?
Step 3--plan a strategy
The approach will be exactly the same as before. That is, the sum of the forces parallel to the ramp is the same as the net force on the rocket. In earlier exercises there were only two forces parallel to the incline. Now the force of the engine (Fe) makes a third. Note that the pink friction force (Ff) and the orange parallel force (![]() ) are down the ramp and therefore will have a negative sign when substitutions are made.
) are down the ramp and therefore will have a negative sign when substitutions are made.
Step 4--carry out the strategy
Σ (parallel forces) = ![]() .
.
Next, substitute for ![]() and Ff, but be mindful that both
and Ff, but be mindful that both ![]() and Ff are down the plane, so, put a "-" in front of the substituted terms.
and Ff are down the plane, so, put a "-" in front of the substituted terms.
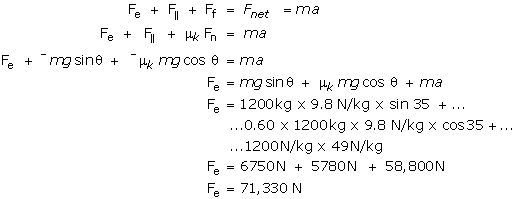
Step 5--communicate
To two significant digits the engine must provide a thrust of
71,000 N.
One more to go...
Practice exercise 7Without pushing at any time, a skier skis down a frictionless 20.0 m slope, hits a frictionless horizontal portion and coasts to a stop a certain distance up another slope where the coefficient of kinetic friction is 0.20. The first slope is inclined at an angle of 35o and the second at 30o. How far up the second incline will she go?
SolutionStep 1--read and understand the story of the problemThe picture really tells the story. We have to find d2, the distance up the second slope. Step 2--list the givens and the unknownd1 = 20.0 m μk1 = 0 θ1 = 35o μk2 = 0.20 θ1 = 30o d2 = ? While d2 is the main unknown we also have to deal with h1 and h2. Step 3--plan a strategyThe key information, at least at the beginning, is that there is no friction on the first slope and on the horizontal portion. We can therefore apply the law of conservation of mechanical energy and say that the kinetic energy at the bottom of the second incline is exactly equal to the gravitational potential energy at the top of the first. On the second incline some of the kinetic energy is "robbed" by friction. This "lost" energy can be calculated because the friction force does work against the motion of the skier. This energy is determined by Wf = Ff x d2. So the kinetic energy at the bottom of the second slope changes into Wf and gravitational potential energy at the top of the second incline. Writing the appropriate equations for the law of conservation of energy will allow the determination of d2. Step 4--carry out the planLet's start by writing expressions for h1 and h2: h1 = d1 sin 35 = 20 m x sin 35 = 11.5 m h2 = d2 sin 30 = 0.5 d2 (this is as far as we can go with h2 because d2 is unknown) Next write the gravitational potential energy equation for the top and bottom of the first incline: (Ek) bottom = (Eg) top (because there is no friction) ½ m v2 = mgh1 which allows the cancellation "m", and that's a good thing because we were not told the mass of the skier. Continuing: v2 = 2gh1 = 2 x 9.8 m/s2 x 11.5 m = 225 m2/s2 . Let's not bother to find the square root of both sides, because as you will see in a moment, it will just be a waste of time. Because the horizontal portion is frictionless, the kinetic energy at the bottom of the second incline is the same as the kinetic energy at the bottom of the first. That is (Ek)bottom 2 = (Ek)bottom 1 = ½ m v2 = ½ m (225 m2/s2) Now write the gravitational potential energy equation for the top and bottom of the second incline. Remember, the kinetic energy at the bottom is transformed into energy lost due to friction (Wf) plus a gain in gravitational potential energy (mgh2). (Ek)bottom 2 = Wf + mgh2 (Ek)bottom 2 = Ff x d2 + mgh2 ½ m (225 m2/s2) = μk2 Fn x d2 + mg (0.5d2) |
|
| To substitute for Fn, see the usual set-up to the right.
Fn = mg cos θ |
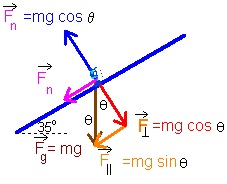 |
|
Which means that ½ m (225 m2/s2) = μk2 Fn x d2 + mg (0.5d2) can be written as ½ m (225 m2/s2) = μk2 mg cos θ x d2 + mg (0.5d2) Again we conveniently cancel the mass "m" and solve for d2: ½ (225 m2/s2) = μk2 x 9.8 m/s2 x cos 35 x d2 + 9.8 m/s2x (0.5d2) 113 m2/s2 = 0.20 x 9.8 m/s2 x 0.819 d2 + 4.9 m/s2 d2 113 m2/s2 = 1.6 m/s2 d2 + 4.9 m/s2 d2 113 m2/s2 = d2 (1.6 m/s2 + 4.9 m/s2) 113 m2/s2 = d2 x 6.5 m/s2 d2 = 113 m2/s2 ÷ 6.5 m/s2 d2 = 17 m Step 5--communicateThe skier comes to a stop 17 m up the second slope. |
|
Activity
Your textbook (Nowikow and others) has several exercises to provide further practice. See 1-4 in "Applying the Concepts" on p. 196, and end-of-chapter exercises for section 6.1 on p. 224. The answers are given at the back of the text. Practice! Practice! Practice!
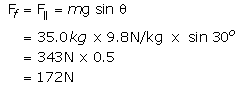 You should be able to see that if we had used
You should be able to see that if we had used