Outcomes
In this lesson you will learn
- the meaning of coordinate rotation
- how to use coordinate rotation to determine the force component that is parallel to an incline and the component that is perpendicular to an incline
- how to apply Newton's second law on an incline in an ideal frictionless environment
- how to apply Newton's second law on an incline when friction is present.
By the way, in the third statement above the word "ideal" is used. Would a frictionless environment be really ideal?
Prerequisites
To be successful in this lesson, you must know how to do the following as described in Section 02, Lesson 01 "Vector Review" and Lesson 02 "Review of Newton's laws of Motion":
- determine gravitational force when mass is given
- apply trigonometric functions to determine perpendicular components of a given force
- apply the forces to produce free body diagrams
- apply kinematics equations and Newton's second law to numerical exercises.
You may want to review these lessons before beginning Lesson 03, or you might decide to refer to the lessons as required.
In addition to the above material, some exercises in this lesson will require you to apply the law of conservation of mechanical energy introduced in Physics 2204. The topic was re-introduced in Lesson 05 of Section 01 of this course. You may wish to refresh your memory before working through the review exercises below. A quick summary is given here.
Gravitational potential energy = Eg = mgh
Kinetic energy = Ek = ½ mv2
Eg + Ek never changes, that is
(Eg + Ek) position 1 = (Eg + Ek) position 2
We should say a few words about units. Look at the right-hand side of the potential energy expression (mgh). This expression can be written as Fgh, so the units are [N·m]. This is an energy unit.
Now look at the right hand side of the kinetic energy expression (½mv2). The units are [kg·m2/s2]. This is also an energy unit. In fact,
[N·m] = [kg·m/s2 x m] = [kg·m2/s2].
That is, the unit of mechanical energy can be broken down in 2 different ways
This unit of energy is called a joule [J].
Review exercise 1
A 65 kg flounder lies precariously on the edge of a wharf that is 2.5 m above the water. If it wiggles over the edge and falls, determine
(a) the gravitational potential energy of the flounder with respect to the top of the water just as it begins its descent.
(b) its kinetic energy just at it splashes into the water
(c) its speed just as it hits the water.
Solution
a)
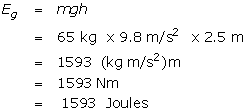
To 2 significant digits the gravitational potential of the flounder on the wharf is 1600 J.
Note that there is no negative in front of the "h" because we are not concerned with the change in height. The gravitational potential energy is calculated for a particular height above some reference level, in this case the water.
b) It helps to realize that the kinetic energy on the wharf, and the potential energy at water level are both 0.0 J. In other words, all of the potential energy at the top is transformed completely into kinetic energy at the bottom (assuming no lost due to the heat of friction).
We say (Ek)water = (Eg)wharf = 1600 J.
c)
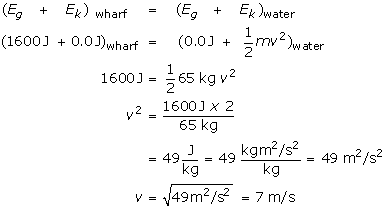
Review exercise 2
A golf ball is hit horizontally from a knoll that is 12.7 m above the level course. It leaves the tee traveling at 27.8 m/s. With what speed does it strike the ground.
Solution
You should be getting déjà vu. This exercise first appeared as a projectile motion problem in Lesson 03 of Section1. Now here we trying to solve it by using the law of conservation of energy and we don't even know the mass of the ball! Never fear. Physics will triumph!
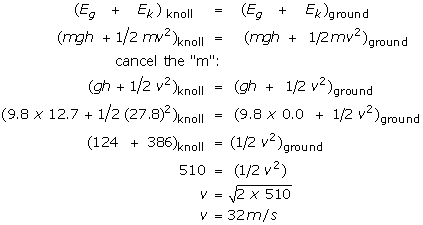
For a good feeling compare this result with the answer to practice exercise 3 in Lesson 03 of Section 01. So, we conclude that the path makes no difference when applying the law of conservation of energy. The important piece of information is the height, not the distance traveled. In this lesson the paths will not be curved, but they will be inclined at some angle with the horizontal, as, for example, an object moving on a ramp.