The Concept of Work

Lesson

If someone asked you how you are doing with your physics course, you would probably say that there is a lot of work to it. Or, you may have had the misfortune of trying to push a car that was stuck in a ditch and then finally having to quit because no matter how you worked you could not budge it. You may be surprised to know that, in the "physics sense", you are not working in either of the above cases. In physics, WORK has a definite meaning. One way of stating the meaning is:

Work is done on an object when a force moves the object a certain distance.

The amount of work done can be calculated. It is the product of the amount of force that causes the motion and the distance through which the force acts:

Work = (force causing motion) x (distance)

W = F_|| d.

Perhaps you are wondering about the "parallel" subscript. This is because forces often act at an angle to the motion and you only wish to consider the part of the force that acts in the direction in which the object moved. After all, forces don't always act exactly in the direction that the object moves. Some of the force is therefore sort-of "wasted" by acting in the wrong direction.

Think about mowing the lawn. You apply the force along the handle, which makes some angle with the horizontal. The amount of force that acts in the direction of motion--and therefore the work done--depends upon the angle that the handle makes with the horizontal. You can use this to write an expression for the work done. Play the animation below to do this.

We could not use all of the applied force to calculate the work done in pushing the mower. The force used had to be THE PART OF THE FORCE THAT WAS PARALLEL TO THE DIRECTION OF MOTION. Can you see what would happen if the handle were to make a larger angle with the ground? Can you see that F_|| will then become smaller and smaller? This means that the amount of work you do will also become smaller and smaller. Once the angle reaches 90^o the applied force is perpendicular to the motion so no work would be done at all.

What is to be learned from all of this?

If a force is to do work on an object, then that force (or some component of the force) MUST BE in the direction that the object moves. The greater the angle between the direction of the force and the direction that the object moves, the smaller will be the work done on the object. If the force is perpendicular to the direction of motion of the object, then the force DOES NO WORK.

Let's try some worked examples to demonstrate how to apply the expression for work.

Let's start with a simple example that demonstrates a very basic application of the equation for work. In Example 1 the angle between the force and the direction of the motion is 0^o. Because cos 0^o = 1 the expression simplifies to

W = F d cos 0^o = F d (1) = F d

W = F d

Notice that the units for work are N m, which are written as joules, J.

In Example 2 the force is not acting exactly in the direction of the motion. You must therefore find the magnitude of the component acting in the direction of motion. This is given by F cos q. The amount of work will therefore be found using

W = F d cos q

There. That wasn't so bad, was it? You are about ready to try a few on your own. The next page of the lesson has two more worked examples. Before trying these, why not first try a few items from the "assigned activities" section?

As you do practice exercises, don't forget that the units of work are joules, which are newton-metres.

Before you proceed any further, it should be pointed out to you that work is a scalar quantity, not a vector. This might confuse you a bit--after all, both force and displacement are vector quantities. Later, if you do some vector algebra after high school you will learn that Work is actually the scalar product (usually called the dot product) of two vectors.

Work is a particularly interesting scalar product in that it can take negative values. This is because the angle q between the force and the direction of motion can actually be a value from 90^o to 180^o. In those instances the applied force is actually opposing the motion. Example 3, which follows, illustrates this.

Take heart if you found Example 3 a bit weird. The concept of "negative work" is confusing to many people! Fortunately there's two bits of good news about this: Bit 1: It's easy to spot when work will be negative. It's when the forceis opposing the motion. Bit 2: After you do the next few lessons and learn more about energy the whole thing will make a lot more sense.

Let's finish the lesson with a slightly harder example. Example 4 shows that kinematics equations can go hand in hand with work.

Example 5 (not an animation)

How much work do you do on a 1200 g bag of sugar in lifting it from your kitchen floor to the counter top which is 72 cm above the floor?

Solution:

You know that W = Fd, but in this case what is the force that you apply? The answer is "the force needed is just the weight of the sugar, which is given by mg." This means the formula becomes W = mgd. The only other thing to watch out for is to change grams to kilograms and centimeters to meters. So,

m = 1200 g = 1.2 kg d = 72 cm = 0.72 m g = 9.8 N/kg

W = Fd = mgd = 1.2 kg x 9.8 N/kg x 0.72 m = 8.5 Nm = 8.5 J

Activity

Assigned activities

Complete the following:
1. Suppose that you spent a whole day holding boards in place while your friend nailed them in place. Why could it be said, at the end of the day, that you did no work?
2. If you were in deep outer space and fired a cannonball it could possibly keep moving forever. Even though it might move for millions of light years, why would it still be true that the only work done was when it was first fired?
Explain why no work is done in each instance:
1. A curling stone moves at a speed of 0.8 m/s for 10.0 m
2. A crane holds a 5.0 tonne girder stationary while it is welded in place.
Use the examples from question 2 above to compare work in the physics sense with the everyday sense of the word.
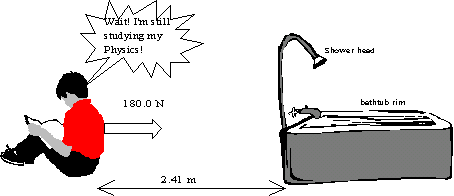
How much WORK will be done in dragging the boy over to the tub?
An front loader raised 2.33 tonnes of dirt from the ground to a height of 3.85 m. How much work was done? Note, 1 tonne, 1 T = 1.0 x 10³ kg.
Calculate the amount of work done in each instance.
1. The coefficient of friction between a sled and the snow is 0.100. The sled has a mass of 50.0 kg and is towed at constant speed by a horizontal force. How much work is done if the sled is towed for a total of 100.0 m? Note: recall that F_fr = mmg.
2. The engines of a jet apply an average force of 2.0 x 10⁴ N while the jet taxis a distance of 455 m along the runway.
3. A car's engine applies the force needed to overcome friction while thecar moves a distance of 75 km at constant speed. The mass of the car is 1400 kg and the coefficient of friction is 0.300.
A 300.0 kg load is dragged horizontally through a distance of 8.20 m. If the total energy expended is 4.32 x 10³ J what force was applied?
A tractor does 8.3 kJ of work towing a crate across a warehouse floor. If the force that did the work was 450 N, then through what distance did the crate move?
Calculate the amount of work done in each instance.
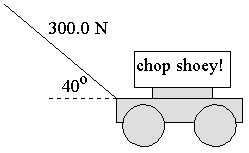
1. A mower handle makes an angle of 40^o with the horizontal. A force of 300.0 N, applied along the handle, causes it to move a total distance of 340 m.
2. The handle of a "snow pusher" makes an angle of 35^o with the horizontal. Every sweep of the blade moves the snow 1.2 m. A force of 220 N is used. How much work is done with each sweep?
You are towing your little sister on a slide. The rope makes an angle of 42^o with the ground. You apply a force of 234 N along the rope. How much work will be done if you tow the sled a distance of 300.0 m?
Under what condition can the amount of work done be negative?
A hockey puck is passed to a player. The player's stick moves back a distance of 0.18 m while "catching" the puck. The average stopping force needed was 1.50 N. Calculate the amount of work done in stopping the puck.
A hockey player runs at the boards, initially traveling at 4.0 m/s. To protect herself she holds out her arms, which she bends as she hits the boards. The boards apply an average stopping force of 1100 N while the player's arms "compress" by 65 cm. How much work is done? Note: assume that the hockey player actually moved 65 cm while stopping.

Answers

4. 434 J 5. 8.79 x 10⁴ J

6. (a) 4900 J (b) 9.1 x 10⁶ J (c) 3.1 x 10⁸ J

7. 530 N 8. 18 m 9. (a) 7.8 x 10⁴ J (b) 216 J