Outcomes
In this lesson you will
- define the physics term work and contrast it with the everyday meaning;
- use the concept of work to solve real-world problems.
Specific Curriculum Outcomes:
- analyse quantitatively the relationships among force, distance, and work;
- analyse quantitatively the relationships among work, time, and power;
- design and carry out an experiment to determine the efficiency of various machines.
Introduction
Section 2 introduces additional concepts: work, power and efficiency. You will contrast the physics concept of work with the everyday usage of the word. You will also use the concepts to solve real-world problems.
Prerequisites
Previously you encountered the newton (N) as the unit of force. Recall that 1 N is the force that will cause a mass of 1 kg to accelerate at 1 m/s2.
In this lesson you will also use some trigonometry. Recall that in a right triangle the cosine of either of the acute angles is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse.

In the figure shown above, AC is the side adjacent to ÐA and BC is the side adjacent to ÐB. You can therefore write
![]()
These expressions can be used to find components. In this lesson you will mostly be using the component that acts in the direction of motion. The diagrams will be drawn so that this is typically the horizontal (x) component.
Example 1
A force of 32.5 N is directed at an angle of 22o above the horizontal. Find the horizontal (x) component of the force.
Solution.
A diagram is important. The figure below depicts the given information.
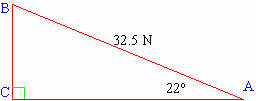
Notice that the horizontal component is represented by side AC, which is the adjacent side. You know therefore to use the cosine ratio.
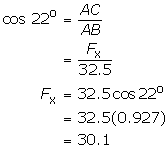
The horizontal component is 30. N (using 2 significant digits).