Lesson

The ability to recognize certain characteristics of the graph of a function simply by looking at its equation is a very important skill. From previous work, you should have this skill for several other functions. 

For example, you learned that the graph of y = mx + b is a straight line and that the slope has value m and the y-intercept is b. 

Similarly, you learned that the graph of y = ax2 + bx + c is a parabola and that its direction, width of opening, and vertical stretch are all determined by the value of a and its y-intercept is c.

In this lesson you will explore graphs of exponential functions of the form where a > 0 (for example ) and b > 0 
().  Investigation 5 explores the characteristics of the graph that are controlled by a and b. Go to your text book now and read through the introduction to Investigation 5 on page 127 before you proceed with the rest of this lesson.

For Step A, use your calculator where necessary and create a table of values like the one shown below for each of the functions. The one below is for the first equation in (a), viz, y = 0.8x

x

-3

-2

-1

0

1

2

3

y

 1.95 1.56 1.25 1 0.8 0.64 0.512

Draw graphs in Step B on your own paper. Put the three graphs for (a) on the same set of axes and the three for (b) on another set of axes. Refer to the note in the side-bar of your textbook recommending that you use different colours for each graph to help distinguish between the functions on your co-ordinate plane. The graph of the table above is shown below:

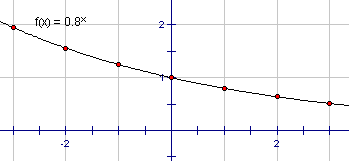
One thing you should also note is that regardless of how large we make x, the function never becomes zero (e.g. 0.830 = 0.001238). The line that the function  approaches, getting closer and closed to but never touching, is called an asymptote to the curve. Since this graph gets closer and closer to the x-axis but never touches it, the x-axis (which has equation y = 0) is its asymptote.

A summary of what you should have discovered by doing the Investigation and answering the Investigation questions is given on the next page. Before you look at it, you should complete the Investigation and try to discover these relationships for yourself.

For exponential functions of the form  y = abx   :

  • The focal point is (0 , a), which means that the y-intercept is a. 
  • When b > 0 , the curve is increasing from left to right and is a growth curve. The larger the value of b, the more rapidly the curve increases.
  • When b < 0 , the curve is decreasing left to right and is a decay curve. The smaller the value of b, the more rapidly the curve decreases.
  • There is no x-intercept but if the graphs are extended far enough to the left for growth curves and to the right for decay curves, the curves will come extremely close to the x-axis; in fact we can get as close to the x-axis as we want by choosing a big or small enough value for x. The x-axis or its equation y = 0 is called an asymptote for the curve.
  • The form 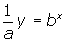is its transformational form of the function and  a gives the vertical stretch of the basic function y = bx .

The Interactive below shows some of these properties for various graphs.

Activity

  1. Complete Investigation 5 on page 127 in your text.
  2. Complete the Investigation Questions 1 - 8 on pages 128 & 129.
  3. Do the CYU Questions 9 - 12 on pages 129 &130.

When you have completed these questions, ask your on-site teacher to get the solutions for you from the Teacher's Resource Binder and check them against your answers. After you do this, if there is something you had trouble with and still do not understand, contact your on-line teacher for help.

Test Yourself

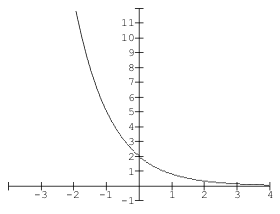
  1.  The graph below has exponential equation y = abx.  Describe the values of a and b.

  2. Without graphing, state the y-intercept and whether the following exponential functions form a growth or decay curve.

        (a)  y = 0.5 (2.5)x                               (b)  y = 2.5 (0.5)x

Solution