Lesson

How many carbon atoms are there in the tip of your pencil? Is it possible to count them? Is there a way of expressing the number of atoms without having to count them one by one?

Mass Measurements as a Convenient Alternative to Counting

Counting is useful when the number of things to be counted is relatively small. In some cases it isn't. Consider this example:

Imagine that you have to make up a materials list for a deck you are building. The list might look like this:

  • 20 pieces of 1" x 6" x 12' pressure treated lumber for decking
  • 10 pieces of 2" x 8" x 12' pressure treated lumber for framing
  • 2 kg  of 3.5" deck screws

You might ask: "Why buy the wood in individual pieces and the screws by the kilogram?" The answer is convenience. It is convenient to count out pieces of wood because relatively few pieces are required; however, in the case of the deck screws, it is easier to measure out a 2 kg amount than it is to count out the large number of screws needed to fasten the boards together.

Substituting a mass amount for a counted amount is a common practice in chemistry because of the impracticalities of counting things as small as atoms and molecules. However, in chemistry (and in carpentry) there's a catch. There's something you need to know before you can substitute mass measurements for counted amounts. Any idea what it might be?

The Catch...

When you measure by mass, how do you know how many items there actually are in a sample? For example, how many 3.5" screws are there in a 2.5 kg sample? If the screws are only 2" long, does a 2.5 kg sample contain more screws? Obviously some sort of conversion factor is needed to convert a mass to a number of items.

Manufacturers of screws supply conversion factors to retailers. In some hardware stores these factors are posted for customers to see. Coming up with these conversion factors is pretty easy. Just add screws one at a time to a balance until you have a 1 kg mass. Knowing how many screws of a certain size makes up 1 kg allows you to convert back and forth between the number and the mass amount. Here's an example.

Can the same process be applied to atoms?

The Mole (Avogadro's Number)

In the case of atoms, the solution is not as simple because counting out enough atoms to make up a kilogram is totally impractical, if not impossible. 

Atoms are so small that it takes an incredibly huge number of them to make up a visible amount. An iron spike for example might contain more than 6.02 x 1023 atoms of iron. Now dealing with exponents may or may not have been your favourite part of math class, but dealing with such large numbers of atoms on a consistent basis can get to be tiresome after a while. That's where the mole comes in.

1 mole of carbon or exactly 12 grams

A mole is the number of carbon-12 atoms in exactly 12 grams of carbon-12. This number was determined by dividing the mass of a single carbon-12 atom into a 12 g mass of carbon-12. Since the mass of a single carbon-12 atom is tiny (1.99 x 10-23 g), the value of a mole comes out to be a huge number: 6.02 x 1023. How big a number is it? Check out these comparisons! 

The mole is not an exact number. Current estimates place its value at 6.022137 ´ 1023. The greater precision (number of decimal places) in the current value is a function of the greater precision of the devices currently used to measure the mass. You will use the value 6.02 x 1023 in your calculations.

At this point, the most important thing to remember about the mole is that it represents a big number - a very, very, very big number. Chemists use it in the same sort of way that a egg farmer uses the dozen.

So instead of dealing with individual atoms and molecules, chemists deal with mole amounts. Unfortunately, there are no measuring devices that give readings in moles. Chemists measure things by mass or volume.

We are still left with this question: How do we get from a convenient substitute for a counted amount (mass) to a counted amount (moles)? 

Molar Mass

In chemistry, the conversion factor is molar mass (the mass of one mole). This value has been calculated for each element and is usually included in a periodic table. In most periodic tables of the elements, the molar mass value is located in the top right hand corner of an element's cell.

The value 55.85 g/mol means that a mole of iron atoms 6.02 x 1023 (atoms) has a mass of 55.85 grams. In the next lesson, you will see how molar mass values can be used to convert mole amounts to mass and vice versa.

Try Exercise 1 in the Assigned Activities section below.

Visualizing Moles

What does a mole (6.02 x 1023) look like? Each of the beakers below contains a mole of atoms. 

         55.85 g Iron         63.55 g Copper       118.69 g Tin         126.90 g  Iodine

The Molar Mass of a Compound

As you know, few elements exist as pure substances in nature - most of them are found in compounds. In fact, most of the substances you will encounter in future lessons are compounds. And, although the periodic table provides you with the molar masses of the elements, it does not provide you with the molar masses of compounds. 

To find the molar mass of a compound, you have to write the chemical formula, list the number of atoms of each element, and multiply this number by the molar mass of the element.

Example 3

Calculate the molar mass of water.

Answer

Write the chemical formula: 

  • H2O

List the number of atoms of each element in the compound:

  • 2 H
  • 1 O

Multiply each number by the molar mass of the element:

Add the products:

Communicate the answer: 

  • The molar mass of H2O is 18.02 g/mol.

(You will be using the molar mass of water frequently, so it is a good idea to memorize it as 18.02 g/mol.)

When calculating the molar mass of a compound, it is important to remember what each numerical subscript is indicating. Numbers to the lower right of an element symbol indicate the number of "atoms" of that element in the compound. Numbers outside the parentheses are used to balance a chemical formula. To determine the number of "atoms" in a formula, you multiply terms inside the parentheses by the ones outside the parentheses. 

Consider the formula: (NH4)3PO4. There are:

  • 3 x 1 nitrogen atoms (a total of 3 N)
  • 3 x 4 hydrogen atoms (a total of 12 H)
  • 1 phosphorus atom
  • 4 oxygen atoms.

Now you try it. List the number of "atoms" of each element in Ca3(PO4)2 . Check your answer .

The key thing to remember is that parentheses have the same meaning in chemistry as they do in math; that is, a value outside a set of parentheses is multiplied by terms inside the parentheses.

Example 4

Calculate the molar mass of barium hydroxide octahydrate.

Answer

Begin by writing the chemical formula for barium hydroxide octahydrate. 

  • Barium forms a 2+ ion because it is a Group 2 element: Ba2+. 
  • Hydroxide is a polyatomic ion with a 1- charge, OH-. 
  • Octahydrate means 8 H2O. 
  • It takes two hydroxide ions to balance the charge on one barium ion, so the chemical formula is Ba(OH)2·8H2O 

Count and list the atoms/ions of each element, but treat water as a unit.

  • 1 Ba
  • 2 O
  • 2 H
  • 8 H2O

Next, look-up the molar mass of each item in the list and multiply. (Remember the molar mass of water is 18.02 g/mol.)

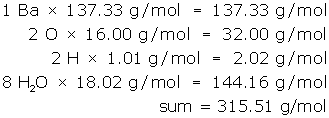
Communicate the answer:

  • The molar mass of barium hydroxide octahydrate is 315.51 g/mol.

As you get comfortable with molar mass calculations, you can combine the steps into a single line like this:

(1 Ba x 137.33) + (2 O x 16.00) + (2 H x 1.01) + (8 H2O x 18.02) = 315.51 g/mol

Always show the unit for molar mass (g/mol) in your final answer. 

You will review the concept of significant digits and rules for rounding as you complete the upcoming lessons. Note that in this course, molar mass values (calculated or listed in tables) ALWAYS show precision to two decimal places. 

Summary

Here is a summary of the steps to complete in molar mass calculations:

  • write the chemical formula for the compound.
  • list the number of particles of each element in the compound.
  • multiply each number in the list by the molar mass.
  • add the products: ALL molar mass values must show precision to TWO decimal places in this course.
  • communicate the answer.

Now you try it. Complete Exercise 2 in the Assigned activities page.

Molar Volume

Another way of measuring amounts of substances is by volume. The SI unit of volume is the litre.

Amounts of gases like hydrogen, helium, nitrogen and oxygen can be measured and compared in litres if the samples are at the same temperature and pressure. The reason for this is that changes in pressure and/or temperature can effect the volume of a gas.

Chemists compare gas volumes at 0°C and 101.3 kPa. These conditions are known as Standard Temperature and Pressure or STP.

Now you've undoubtedly heard the saying "light as air". Most people think that air has little or no weight (mass) - nothing is further from the truth! There is a tremendous mass of air on your shoulders! You just don't notice it because you have been bearing it since you were born.

The reason that gases appear to be lighter than liquids or solids is that they are less dense. Compare the density of iron and hydrogen (pay attention to the density units for solids versus gases in your periodic table)!

                 

Hydrogen is much less dense (0.0899 g/L versus 7.87 g/mL)!

What does all of this mean? Well in a gas sample, the particles are really spread out - there is a lot of empty space between them. The same is not true for solids and liquids. It turns out that gas volumes contain a consistent number of gas particles regardless of the type of gas! This idea was proposed by Amadeo Avogadro in 1811.

Based on what was known about how gas volumes combined in chemical reactions, Amadeo Avogadro concluded that equal volumes of different gases at the same temperature and temperature, have the same number of particles (i.e. same number of moles)!

This very significant discovery led to the concept of molar volume:

1 mol of any gas at STP has a volume of 22.4 L.

You should memorize the value 22.4 L/mol as molar volume at STP, but in the event that you forget it, you can look it up in the table on the data side of your periodic table - you will see it listed in the middle column under the heading "Measured (Uncertain) Quantities".

Why "uncertain"? Well it turns out that there is a little variance in molar volume from one gas to another, but not that much - we can apply the value 22.4 L/mol with confidence in this course.

Activity

Textbook Readings

MHR
  • pages:  47 - 49:  The Avagadro Constant and the mole.
  • pages:  55 - 56:  Molar mass.
  • pages:  69: (definition: molar volume)

Textbook Items

MHR
  • page 54:  # 1
  • page 57:  # 16 - 19 (watch the brackets in formulas!)
  • page 76:  # 16

Practice Items

Exercise 1

  1. How many particles are there in a mole?
  2. How many atoms of sodium are there in one mole?
  3. What is the mass of one mole of sodium atoms?

Exercise 2

Calculate the molar mass of each compound.

  1. NaHCO3
  2. Sr(NO3)2
  3. Al2(SO4)3 
  4. CuSO4
  5. FeSO4·3H2O
  6. lead(II) acetate
  7. magnesium chloride

Exercise 3

  1. What does STP mean?
  2. What is molar volume at STP?
  3. What is the volume of one mole of fluorine gas at STP?
  4. What is the volume of one mole of chlorine gas at STP?
  5. Compare the answers for items (b) and (c).

Check your work here.

Test Yourself