Investigation 2: Number Patterns that Grow, Part 2

Test yourself (Answers)

1. t_n = 2n - 3
   
   t₁ = 2(1) - 3 = 2 - 3 = -1;  t₂ = 2(2) - 3 = 4 - 3 = 1; etc.  You could also use your calculator which gives:
   
                         
   
   Sequence = {-1 , 1, 3, 5, 7, 9, 11, 13, 15, 17}
   
   D1 = {2 , 2 , 2, ... , 2, 2}
   
   The constant difference is at level 1 and the generating function is first degree (linear).
   
   
2. t_n = 2n² - n + 3
   
   t₁ = 2(1)² - 1 + 3 = 4;  t2 = 2(2)² - 2 + 3 = 9; etc. Again, using the calculator we get:
   
                       
   
   
   Sequence = {4, 9, 18, 31, 48, 69, 94, 123, 156, 193}
   
   D₁ = {5 , 9 , 13, 17, 21, 25, 29, 33, 37}
   
   D₂ = {4, 4, 4, 4, ..., 4}
   
   The constant difference is at level 2 and the generating function is second degree (quadratic).
   
   
3. t_n = 2n³ - 7n
   
   t₁ = 2(1)³ - 7(1) = 2 - 7 = -5;  t2 = 2(2)³ - 7(2) = 16 - 14 = 2; etc.  Again using the calculator we get:
   
                      
   
   
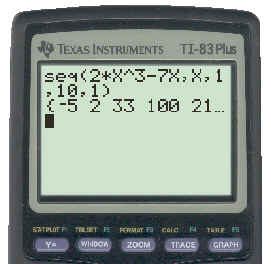
   sequence = {-5 , 2 , 33 , 100 , 215, 390, 637 , 968, 1395, 1930}
   
   D₁ = { 7 , 31,  67 , 115 , 175, 247 , 331, 427 , 535}
   
   D₂ = {24 , 36, 48, 60 , 72 , 84 , 96 , 108}
   
   D3 = {12, 12, 12, ..., 12}
   
   The constant difference is at level 3 and the generating function is third degree (cubic).