are the first four elements of row 15 of Pascal's Triangle.1. The coefficients of the first four terms of the expanded version of
are the first four elements of row 15 of Pascal's Triangle.
The first element of any row of Pascal's Triangle is always 1 and the second element is always the row number. Thus the first coefficient is 1 and the second coefficient is 15.
From our previous work on the relation between Pascal's Triangle and combinations, we know that the first four elements in row 15 are 15C0 , 15C1 , 15C2 , 15C3 . As noted in the paragraph above, we already know the values for 15C0 and 15C1 (you can double check if you like by working out their value using the formula for combinations).
All we have to do is calculate 15C2 and 15C3 :
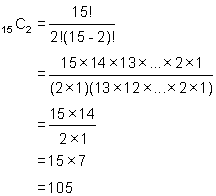
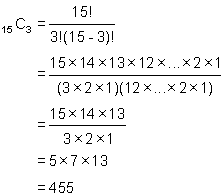
Thus the first four terms of the expansion are:
(x + 1)15 = x15 +15x14 + 105x13 + 455x12 + .....
2.
(3x - 2)5 = 5C0(3x)5 + 5C1(3x)4(-2) + 5C2(3x)3(-2)2 + 5C3(3x)2(-2)3 +You can calculate the combinations using the formula or you can read them from row 5 of Pascal's Triangle. Either way you should end up with:
(3x - 2)5 = 1(3x)5 + 5(3x)4(-2) + 10(3x)3(-2)2 +10(3x)2(-2)3 + 5(3x)(-2)4 + 1(-2)5
(3x - 2)5 = 243x5 - 810x4 + 1080x3 - 720 x2 + 240x - 32
Note the sign change depending on whether the negative term is raised to an odd or even power.