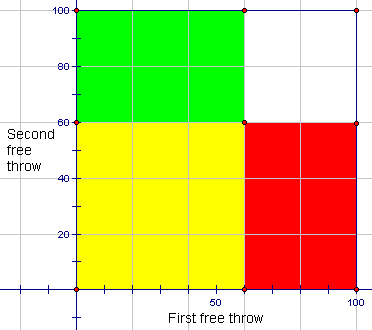
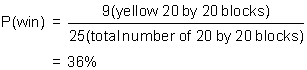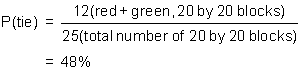Let event A be "You make the first free throw" and let event B be "You make the second free throw". On grid paper set up a set of axes and let event A be recorded along the x-axis and event B be recorded along the y-axis.

Shade an area extending to the 60% mark along the x-axis and the full length of the y-axis (yellow and green areas). Shade an area extending to the 60% mark along the y-axis and the full length of the x-axis (yellow and red area).

1. To win the game you have to make both free throws. You thus have to find P(A and B). In the diagram A and B are represented by the yellow region. The ratio of the yellow area to the total area is P(A and B). For this ratio you can use area units, the larger 20 by 20 blocks, or the actual percentages.
             
   
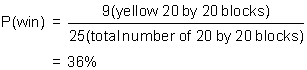
2. You can tie the game by making either of the two throws, but not both as this would be a win. This is the ratio of red (first shot only) and green (second shot only) areas to the total area.
   
             
   
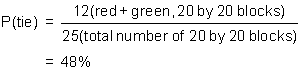
3. To lose the game you will have to miss both shots. This probability is the ratio of the un-coloured area to the total area.
   
               
   
   Alternately. you could notice that the probability you will lose is the complement of a tie or a win. The probability of a tie or a win (mutually exclusive events) is the sum of the two probabilities, 36% + 48% or 84%. The probability of the complement is thus 100% - 84% or 16%